2 Review of PMIC

This section is based on Atallah et al. [2]. The reader might also want to consult [8,9,13,16].

The detection of the above-mentioned approximate repetitiveness is done by approximate pattern matching, whence the name Pattern Matching Image Compression (PMIC). The main idea behind it is a lossy extension of the Lempel-Ziv data compression scheme in which one searches for the longest prefix of an uncompressed file that approximately occurs in the already processed file. The distance measure subtending the notion of approximate occurrence can be the Hamming distance, or of the square error distortion, or the string edit distance, or any of the other distances considered in the distortion theory (cf. [3]).

In short, let us consider a stationary and ergodic sequence $\{X_k\}_{k=1}^\infty$ taking values in a finite alphabet ${\cal A}$ (think of $\{X_k\}$ as an image scanned row by row). For image compression the alphabet ${\cal A}$ has size $\vert{\cal A}\vert=256$. We write X_mⁿ to denote $X_mX_{m+1}\ldots X_n$, and for simplicity $X^n = X_1 \ldots X_n$. The substring X₁ⁿ will be called database sequence or training sequence. We encode X₁ⁿ into a compression code C_n, and the decoder produces an estimate $\hat{X}_1^n$ of X₁ⁿ. As a fidelity measure, we consider any distortion function $d(\cdot, \cdot)$ that is subadditive, and that is a single-letter fidelity measures, that is, such that $d(x^n,\hat{x}^n)=\frac 1n \sum_{i=1}^n d(x_i,\hat{x}_i)$. Examples of fidelity measures satisfying the above conditions are: Hamming distance, and the square error distortion where $d( x_i , \hat{x}_i ) = (x_i -\hat{x}_i)^2$. As in uczak and Szpankowski [8,9] we define the depth L_n as the length of the longest prefix of $X_{n+1}^\infty$ (i.e., uncompressed image) that approximately occurs in the database (i.e., already compressed image). More precisely, for a given $0\leq D\leq 1$ we define: Let L_n be the length k of the longest prefix of $X_{n+1}^\infty$ for which there exists i, $1\leq i\leq n-k+1$, such that $d(X_i^{i-1+k},X_{n+1}^{n+k})\leq D$ where D is the maximum distortion level.

A variable-length compression code can be designed based on L_n. The code is a pair (pointer to a position i, length of L_n), if a sufficiently long L_n is found. Otherwise we leave the next L_n symbols uncompressed. We clearly need $\log n + \log L_n$ bits for the above code. The compression ratio r can be approximated by

 

$$r={{\mathrm overhead~ information} \over {\mathrm length ~of~repeated ~subword}}= {{\log n + \log L_n} \over L_n} ~,$$ (1)

and to estimate it one needs to find out probabilistic behavior of L_n. In [8,9] it is proved that $L_n \sim {1\over r_0(D)} \log n$where r₀(D) is the so called generalized Rényi entropy (which could be views as follows: the probability of a typical ball in ${\cal A}^n$ of radius D is approximately 2^{-n r₀(D)}). From (1) we conclude that the compression ratio r is asymptotically equal to r₀(D).

The above main idea is enhanced by several observations that constitute PMIC scheme. They are:

Additive Shift. It is reasonable to expect that in an image there are several substrings, say x^m, y^m, that differ only by almost constant pattern, that is, y_i=x_i +c for $1\leq i \leq m$ where c is not necessary a constant, but whose variation is rather small.

In such a case we store the average difference c as well as a (pointer,length) pair, which enables us to recover y_i from x_i (instead of storing y_i explicitly). In general, we determine the additive shift c by checking whether the following condition is fulfilled or not

$${1\over m} \left(\sum_{i=1}^m (x_i-y_i)^2 -{1\over m} \left(\sum_{i=1}^m (x_i-y_i)\right)^2 \right) \leq D'$$

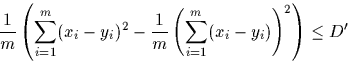
where D' is a constant. If the above holds, we compute the shift c as $c={1\over m} \sum_{i=1}^m (x_i-y_i)$. It can be easily verified that for x_i=y_i+c, and c a constant, the above procedure returns c. In passing, we should observe that this enhancement improves even lossless (D=0) image compression based on the Lempel-Ziv scheme.

Reverse Prefix. We check for similarities between a substring in the uncompressed file and a reversed (i.e., read backward) substring in the database.

Variable Maximum Distortion. It is well known that human vision can easily distinguish an ``undesired'' pattern in a low frequency (constant) background while the same pattern might be almost invisible to humans in high frequency (quickly varying) background.

Therefore, we used a low value of maximum distortion, say D₁, for slowly varying background, and a high value, say D₂, for quickly varying background. We automatically recognize these two different situations by using the derivative ${\cal D}_{ij}$ of the image that is defined as

$${\cal D}_{ij} ={(x_{i+1,j}-x_{ij})+(x_{i,j+1}-x_{ij}) \over 2}$$

where x_ij is the value of (i,j) pixel. In our implementation, we used the lower value of D whenever ${\cal D}_{ij}\leq 3$ and the higher value of D otherwise.

Max-Difference Constraint. Our code will also satisfy the additional constraint that $\vert x_i - \hat{x}_i \vert \leq DD$ where DD is a suitably chosen value. This additional constraint, which we call max-difference constraint, ensures that visually noticeable ``spikes'' are not averaged out of existence by the smoothing effect of the square error distortion constraint. We incorporate this max-difference constraint in the function $d(\cdot, \cdot)$ by adopting the convention that $d( x_i , \hat{x}_i ) = + \infty$ if $\vert x_i - \hat{x}_i \vert \gt DD$, otherwise $d( x_i , \hat{x}_i )$ is the standard distortion as defined above (i.e., Hamming or square of difference).

Small Prefix. It does not make too much sense to store a (pointer,position) when the longest prefix is small. In this case, we store the original pixels of the image.

Run-Length Coding. For those parts of the picture that do not vary at all, or vary little, we used run-length coding: if the next pixels vary little, we store a pixel value and the number of repetitions.

(a) (b)

(c) (d)

Figure 1: Different flavors of PMIC on the ``Lena'' image

Comparisons of different flavors of PMIC on the ``Lena'' image: (a) Classical PMIC (compression ratio equal to 4.3); (b) JPEG (compression ratio equal to 7.9); (c) PMIC with simple predictive coding (compression ratio equal to 7.9); (d) PMIC with column compression (compression equal to 5.3). As mentioned above, in this paper we investigate an impact of prediction algorithms on PMIC. A simple prediction enhancement can work as follows (prediction loop - our main contribution of this paper - is described in depth in next sections):

Prediction. A significant speed up in compression without major deterioration in quality can be obtained by using prediction. It works as follows: we compressed only every second row of an image, and when decompressed we restore the missing row by using a prediction (cf. [11], and next sections). For high quality image compression, one can design a two-rounds approach where in the second round one sends the missing rows. Figure 1 shows two versions of the compressed Lena picture: one with PMIC, and the other with PMIC and predictive ``reduction/expansion''.

Finally, we also explore in this paper one more feature, namely:

Column compression. PMIC is performed on rows. In order to have it performed on columns, one simple way to proceed is to ``transpose'' the original image before compression. Indeed, the rows of the compressed ``transposed'' image are the columns of the original one. This algorithm has been performed on several different images, and this feature can sometimes increase either the compression ratio or the quality level, as shown in Figure 1.

Let us discuss algorithmic challenges of PMIC. It boils down to an efficient implementation of finding the longest prefix of length L_n in yet uncompressed file. We present below one possible implementation (for others the reader is refereed to [2]. Let x₁ⁿ denote the database, y₁^m=x_n+1^n+m denote the yet uncompressed file. As before, we write d(x_i,y_j) for a distortion measure between two symbols, where $d(\cdot, \cdot)$ is understood to incorporate the max-difference criterion discussed earlier.

Algorithm PREFIX
Input: x₁ⁿ and y₁^m
Output: Largest integer k such that, for some index t ($1 \leq t \leq n-m$), $d ( x_t^{t+k-1} , y_1^k ) \leq D$. The algorithm outputs both k and t.
Method: We compute, for all i,j S_ij = total distortion measure between x_i^i+j-1 and y₁^j.

begin
		 Initialize all Sij := 0.
		 for i=1 to n-m do
		 		 for j=1 to m do
		 		 		 Compute Sij := Si,j-1 + d(xi+j-1, yj)
		 		 doend
		  doend
		  Let k be the largest j such that $S_{ij} \leq j D$,         and let t be the corresponding i
		  Output k and t
end

The above can easily be modified to incorporate the enhancements discussed above (additive shift, etc.) and to use O(1) variables rather than the S_ij array.

In order to compress an $N\times N$ image we apply PREFIX several times to compress a row, which we call COMPRESS_ROW algorithm, and this is further use to compress a whole image in either COMPRESS_LONG_DATABASE (where the database sequence is of multiplicity of N, i.e., f N where f is a small integer) or COMPRESS_SHORT_DATABASE (where the database sequence is of length O(1) but located just above the ``point'' of compression). In the former case the algorithmic complexity of compression is O(N⁴) while in the latter case it is $O(n^2\log N)$ which is only $\log N$ away from the optimal complexity O(N²). In this paper we only use COMPRESS_SHORT_DATABASE algorithm.