C Bouclage de phase

  Dans notre montage, le bouclage de phase intervient deux fois; d'abord pour la restitution du signal d'horloge à partir du signal numérique transmis, puis pour la démodulation FSK. Nous allons ici en montrer le principe et l'illustrer avec l'exemple de la démodulation FSK.

Figure C.1: Schéma de principe du bouclage de phase

 A l'entrée du montage de la figure C.1 arrive un signal sinusoïdal (le signal à démoduler) de pulsation $\omega$. Ce dernier est mélangé (multiplié) à celui s' de sortie du VCO (Voltage Controlled Oscillator), ce qui donne un signal de deux composantes sinusoïdales dont les pulsations sont la somme et la différence des pulsations des signaux d'entrée. A la suite du passage du filtre, seule la composante correspondant à la différence des pulsations $\omega - \omega '$ est retenue, pour ensuite être réinjectée à l'entrée du VCO. Ainsi, c'est bien l'écart en fréquences qui, par rétroaction, conduit le système à un retour à l'équilibre, i.e., à une égalité entre la fréquence du signal transmis s et celle du signal e' à l'entrée du VCO, ce qui détermine par conséquent l'amplitude de ce dernier. Dans le cas de la démodulation FSK, le signal transmis ne possède que deux fréquences (f₀ et f₁), ce qui détermine donc pour le signal d'entrée du VCO les deux amplitudes différentes (l'état haut et l'état bas) correspondant au signal binaire d'avant modulation.

Avec les notations de la figure C.1, on obtient:

$$\begin{array} {c} s=s_0\cos \omega t\ s'=s_0'\cos (\omega '... ...2\mbox{, }\beta \mbox{ étant le gain du multiplieur}\end{array}$$

L'équilibre se traduit par $\omega=\omega'$, ce qui implique:

$$\left\{ \begin{array} {lcr} e' & = & K \cos \phi \ \omega -... ...\phi &=& \frac{\omega - \omega _0'}{\alpha K}\end{array}\right.$$

Figure C.2: Marche vers l'équilibre de la boucle de phase

 La figure C.2 montre la marche vers l'équilibre de la boucle de phase. Sans entrer dans les détails d'une démonstration rigoureuse, on peut toutefois avoir une compréhension intuitive de ce qu'il se passe. Sur la figure (dont l'abscisse est le temps et l'ordonnée la pulsation $\omega'$, i.e., à une affinité près, le signal d'entrée e' du VCO) sont montrées, d'une part une droite horizontale correspondant à la fréquence constante du signal transmis s, d'autre part une sinusoïde représentant la pulsation du signal de sortie s' du VCO lorsque le signal d'entrée e' de ce dernier est de fréquence constante (et valant, sur le schéma, $\omega_0'$, c'est-à-dire la pulsation initiale de la sortie du VCO). Enfin, une dernière courbe représente la marche de la pulsation $\omega'$ vers sa valeur d'équilibre $\omega$.

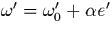Partons de l'instant t=0 et $\omega'=\omega_0'$. On a donc $e'=K\cos\left[ \left(\omega - \omega '(0)\right) t-\phi\right]$. Dès lors, comme $\omega '=\omega_0'+\alpha e'$, $\omega'$ va augmenter en suivant la sinusoïde. e' vaut donc maintenant $e'=K\cos\left[ \left(\omega - \omega '(t)\right) t-\phi\right]$, ce qui correspond à une sinusoïde de période plus grande que celle dessinée, et c'est cette dernière sinusoïde que $\omega'$ va maintenant suivre. Mais comme $\omega'$ continue d'augmenter, la période de la sinusoïde continue elle aussi de croître, ce qui fait augmenter $\omega'$ de moins en moins vite jusqu'à sa valeur asymptotique, qui est sa valeur d'équilibre $\omega$.

Remarquons que nous avons fait partir notre sinusoïde d'une valeur nulle, alors que ceci n'est absolument pas obligatoire. Le raisonnement resterait toutefois analogue, et l'on montrerait de même qu'il y aurait convergence, quitte à passer par une brève phase transitoire de divergence (ce cas se présente lorsque, par rapport à $\omega_0'$, la sinusoïde ne part pas du côté de $\omega$).